Monte-Carlo simulation

A Monte Carlo method is a technique that uses random numbers and probability to solve complex problems. The Monte Carlo simulation, or probability simulation, is a technique used to understand the impact of risk and uncertainty in financial sectors, project management, costs, and other forecasting machine learning models. Risk analysis is part of almost every decision we make, as we constantly face uncertainty, ambiguity, and variability in our lives. Moreover, even though we have unprecedented access to information, we cannot accurately predict the future. The Monte Carlo simulation allows us to see all the possible outcomes of our decisions and assess risk impact, in consequence allowing better decision making under uncertainty. In this article, we will go through 2 differents examples to understand the Monte Carlo Simulation method.

Coin Flip

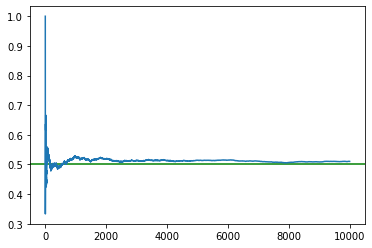
The probability of head for a fair coin is 1/2. However, is there any way we can prove it experimentally? In this example, we are going to use the Monte-Carlo method to simulate the coin-flipping iteratively 10000 times to find out why the probability of a head or tail is always 1/2. If we repeat this coin flipping many, many more times, then we can achieve higher accuracy on an exact answer for our probability value.

import math
import random
import numpy as np
import matplotlib.pyplot as plt

def coin_flip():
  return random.randint(0,1)
  
def monte_carlo(N):
  l=0
  result=[]
  for i in range(N):
    l+=coin_flip()
    prob=l/(i+1)
    result.append(prob)
  return result

N=10000
plt.axhline(0.5,color='green',linestyle='-')
plt.plot(monte_carlo(N))
plt.show()

Monty Hall problem

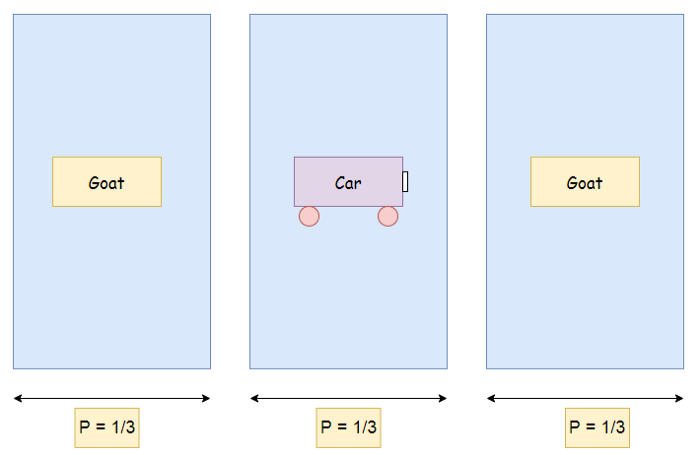
Suppose you are on a game show, and you have the choice of picking one of three doors: Behind one door is a car; behind the other doors, goats. You pick a door, let’s say door 1, and the host, who knows what’s behind the doors, opens another door, say door 3, which has a goat. The host then asks you: do you want to stick with your choice or choose another door?

Initially, for all three gates, the probability (P) of getting the car is the same (P = 1/3).

Now assume that the contestant chooses door 1. Next, the host opens the third door, which has a goat. Next, the host asks the contestant if he/she wants to switch the doors?

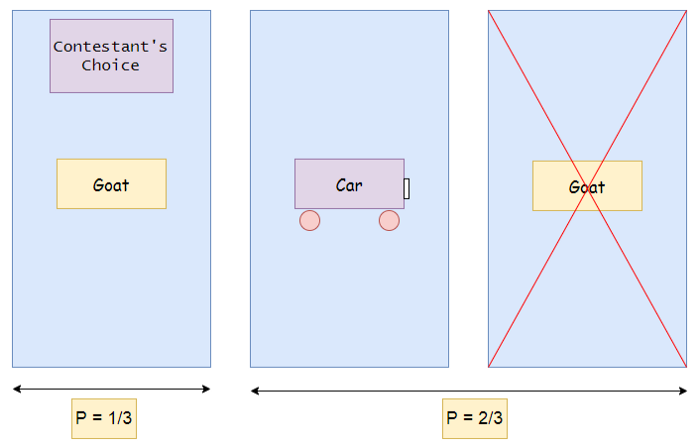
Let’s take a look at each case :

• Not swapping : it means that we will stick with our initial choice which has the probability of 1/3 being a car and 2/3 being a goat.
• Swapping : in this case, the probability of picking a car after swapping is equal to the probability of picking a goat before swapping which is equal to 2/3.

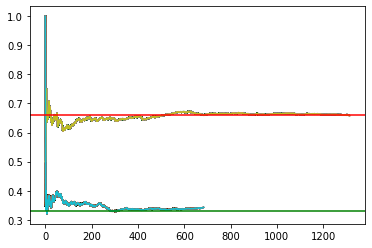
So the best choice would be to always swap doors as it gives you the probability of 2/3 of picking a car.

Now we are going to use the Monte Carlo Method to perform this test case many times and find out its probabilities in an experimental way.

def monty_hall(n):

  doors=['goat','car','goat']
  won_with_swap=0
  swap_prob=[]
  won_with_not_swap=0
  notswap_prob=[]
  
  for i in range(n):
    random.shuffle(doors)
    choice=random.randrange(2)
    
    if doors[choice]!='car':
      won_with_swap+=1
      swap_prob.append(won_with_swap/(i+1))

    else:
      won_with_not_swap+=1 
      notswap_prob.append(won_with_not_swap/(i+1))
      
    plt.plot(swap_prob)
    plt.plot(notswap_prob)
    
  plt.axhline(0.33,color='green',linestyle='-')
  plt.axhline(0.66,color='red',linestyle='-')
  
monty_hall(2000)

Conclusion

It is important to remember that the Monte Carlo Simulation only represents probabilities and not certainty. Nevertheless, the Monte Carlo simulation can be a valuable tool when forecasting an unknown future.

References

• Georges-Louis Leclerc, Comte de Buffon, Wikipedia
• Monte Carlo Simulation An In-depth Tutorial with Python, Medium